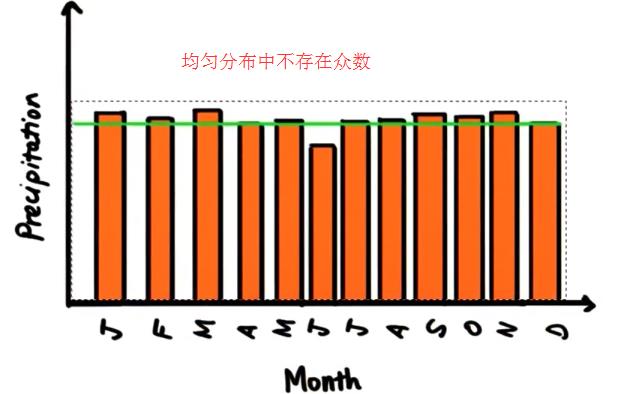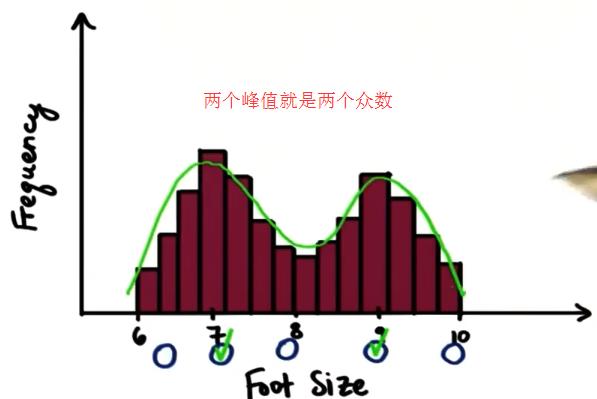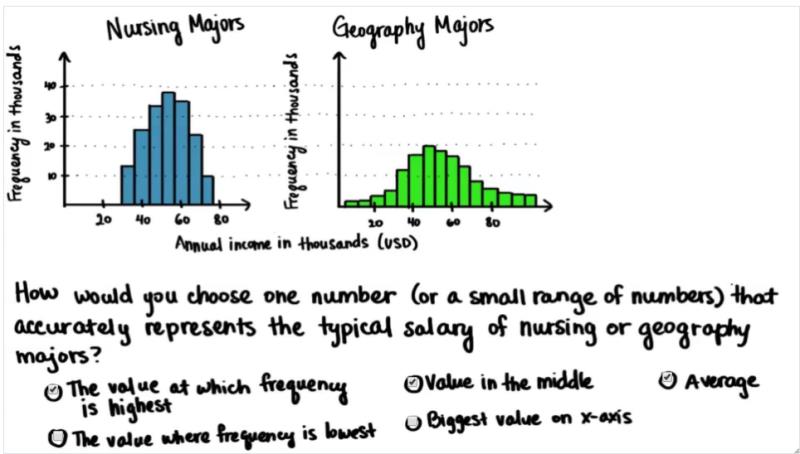
在一个频率直方图中,最能精确代表一个平均范围或最能代表这组数据的是:出现频率最高的值、分布在中间的值、平均值。
众数—出现频率最高的值
英文:mode
- 众数,也就是频率最高的范围(分组),因为无法看出单个值,看到的是一个分组。它出现在X轴上,是最高频率处的任何值。
- 众数可用于描述任何数据类型,数值型和类别型都可以
- 并不是数据集中的所有分值都会影响众数,只有众数的多少才会影响众数
- 在直方图中,众数与呈现数据的方式有很大关系,改变组距会影响众数
- 众数不能代表总体的分布,众数只能说明样本中出现最多的数据
- 众数没有一个计算公式,是通过观察样本或直方图的分布来得出
- 负偏斜分布中,众数也是频率最高的分组
- 对于均匀分布的图形来说,没有众数
- 分类数据的众数
- x轴上出现次数最高的值
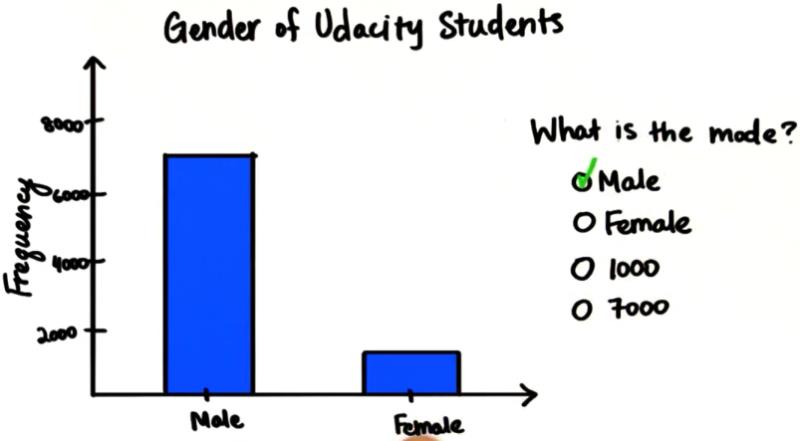
中位数—分布在中间的值
英文:median
中位数,有一半的数据小于这个值,一半的数据大于这个值
为了让中位数更有用,应该按顺序排列好数据
样本量为奇数时,中位数为排序后的中间值
样本量为偶数时,中位数为排序后的中间两个数字,再取中间值
在处理高偏斜分布时,中位数能更好的反应集中趋势
计算
n为偶数:中位数为中间两个数字的和除以2。
n为奇数:中位数为最中间的一个数。

平均值
英文:mean
- 所有数值的和除以数值的个数

- 特性
- 分布中的所有分值都影响平均值
- 平均值可用公式来描述
- 同一个总体中的多个样本会有相似的平均值
- 一个样本的平均值可以用来推论其所在的总体
- 如果向数据集中添加一个极值,它的平均值会发生改变
- 注意
- 出现异常数据时,平均值会有误导性
- 异常数据会把平均值拉向异常数值方向,造成偏斜分布
- 此时的平均值不具备数据中位数的代表性
总结
异常数据对中位数和众数的影响不会很大,但是对平均数的影响却很大。
众数不受异常数据的影响,添加异常数值后中位数几乎没什么变化。
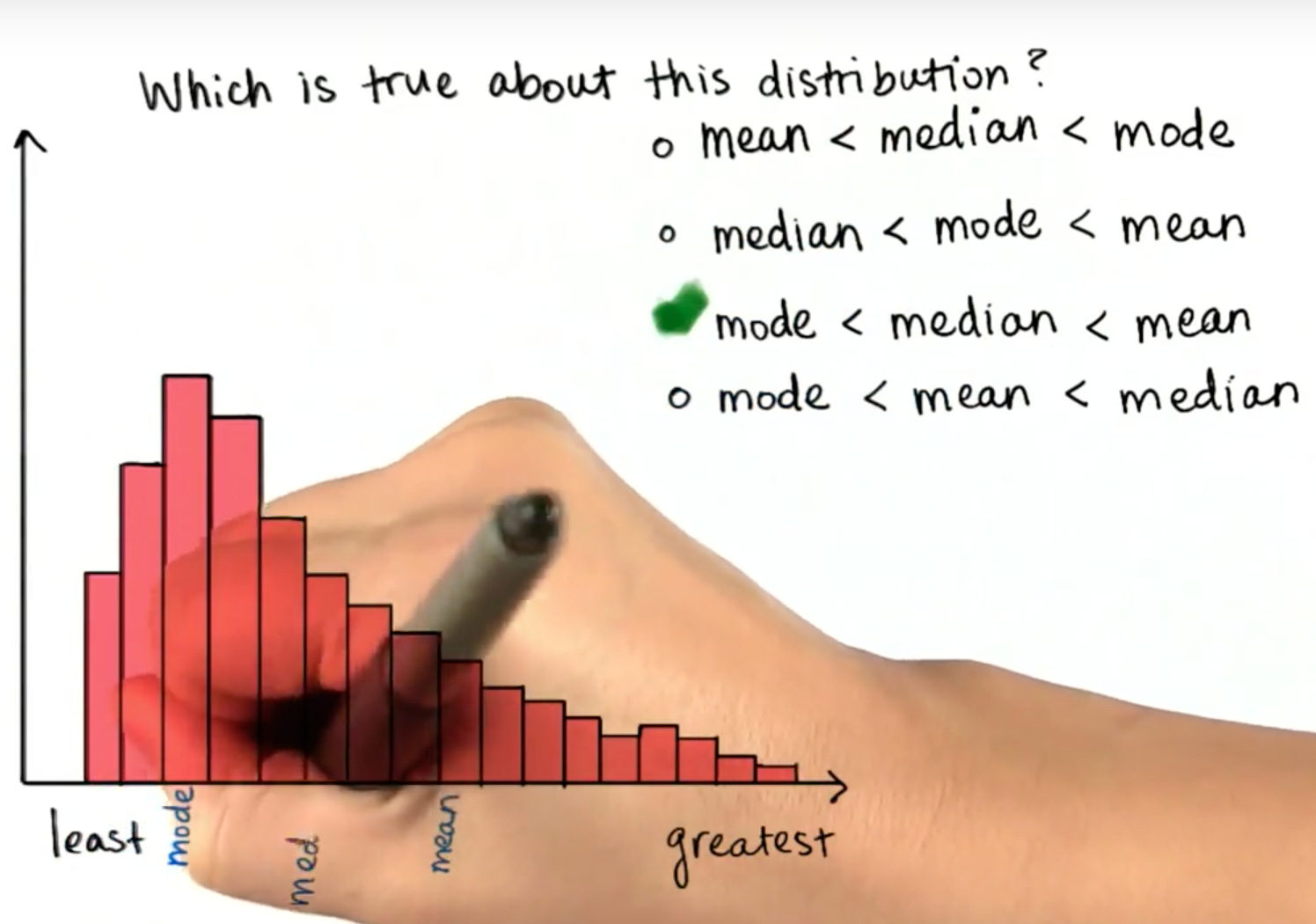
偏态分布
在本图中,众数最小;
因为柱状图的右侧值更大,也就是说有很多大的数据,平均数当然也就更大,肯定大于中位数;
中位数等量分割样本,图形左侧显然样本量多一些,中位数自然也就更接近左侧。
所以,众数最小,中位数居中,平均数最大。
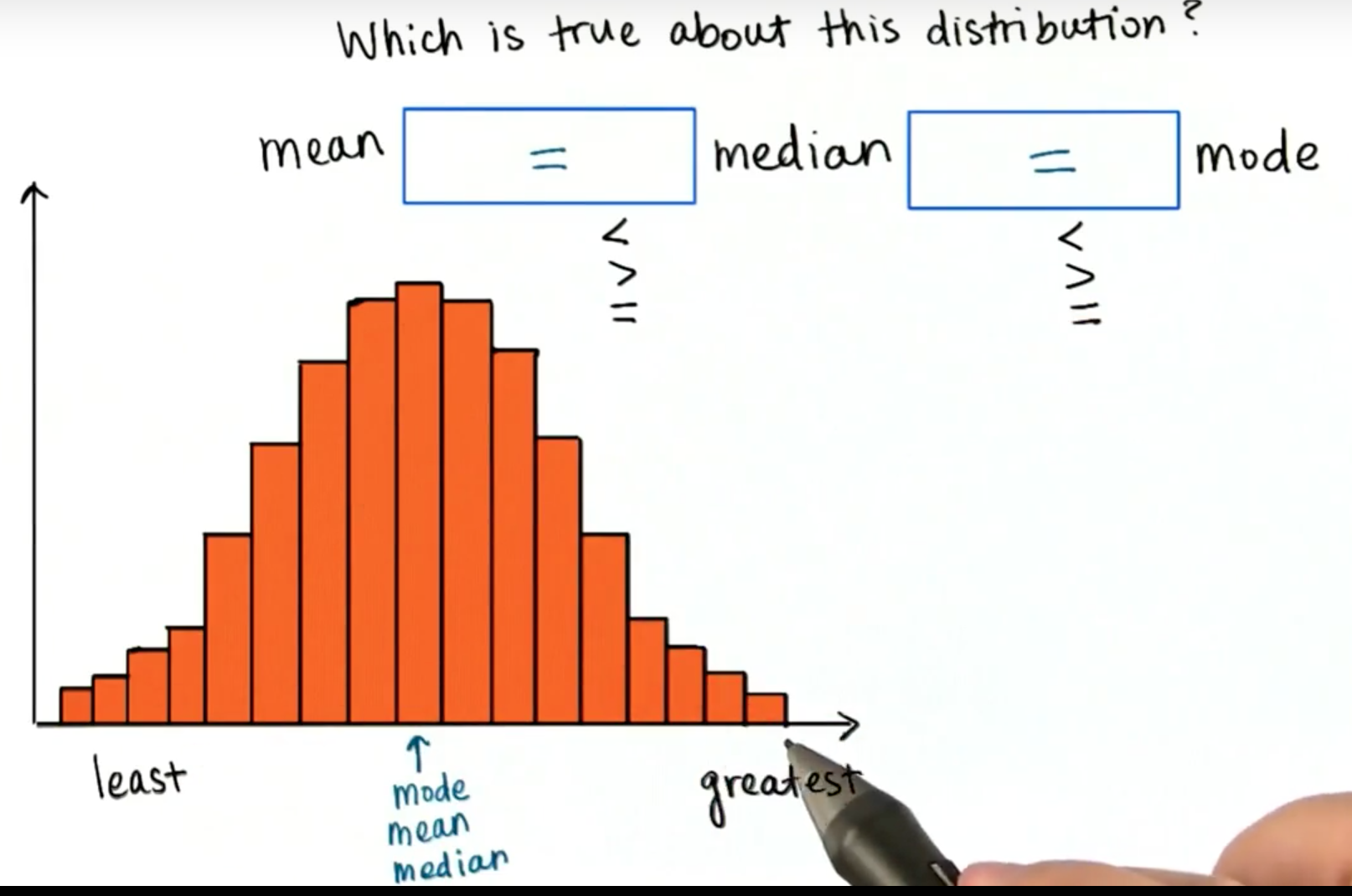
正态分布
图形左右对称,中位数当然居于中间;
中间柱状图最高,也就是众数;
沿X轴往右逐渐增大,也就意味着最中间的值是最平均的。
因此,均值 = 中位数 = 众数。
均值、中位数、众数比较

上图中的表格,翻译如下:
| | A | B | C | D | E |
| ——— | —— | —— | —— | —— | —— |
| 平均数 | ✔️ | ✔️ | ✔️ | | |
| 中位数 | | | ✔️ | ✔️ | |
| 众数 | | | | ✔️ | ✔️ |- A: 有一个简单的公式
- B: 如果数据集中有数据的值变化,它也一定会变化
- C: 不受组距变化的影响
- D: 不易受到异常值的影响
- E: 容易在直方图上找到