我对课程中附带的文档做了大意翻译,当然也借助于Google Translate。
我们总共有三种测量分布中心的方法:
- 算术平均数或数据的均值
- 中位数
- 众数
让我们仔细看看这三点。
平均数
如果我们的数据集近似对称,并且不包含异常值,那么平均数或数据集的均值就适用于中心测量。
平均数的公式 $\frac{\sum_{i=1}^{n} {x_i}}{n}$ .这个公式告诉我们把数据集中所有的值相加,然后除以相加的值的数量。
平均数非常容易受到异常数据值的影响。最大异常值总会把平均值拉向异常值的方向。
中位数
当数据中出现异常值时,中位数最适用于中心测量。这是因为中位数不会受到相当小或相当大的观察体的影响。
中位数是一个数据点,有50%的数据高于它并且50%的数据低于它。为了从一个有n个数据的数据集中找到中位数的位置,我们应该分别考虑两种情况:
数据集中有奇数个的观察体数量
a. 如果是这种情况的话,我们可以用 $\frac{n+1}2$ 来找到中位数的位置。
数据集中有偶数个的观察体数量
a. 在这种情况下,我们找到中间的两个观察体数据并且取它俩的平均值。
中位数的例子:
用这个数据集作为一个例子:

为了找到中位数,采取的第一步就是对我们的数据集进行排序:

在这个例子中,因为 $n=11$ ,所以我们可以用 $\frac{n+1}2$ 来找到中位数,在本例中就是6。所以,我们可以在数据集中数到第6个观察体数据,恰好就是数字8。

如果我们有10个观察体数据,我们应该取中间两个数的平均数。

这就会取到我们的中位数7.5。
众数
这种中心测量最适用于分析目录型数据集。这个数字就是数字、数字范围或目录中出现频率最高的那个。
众数也不容易受到异常数据的影响,因为众数依赖于出现次数最多的观察体,而不是实际的观察体的值。
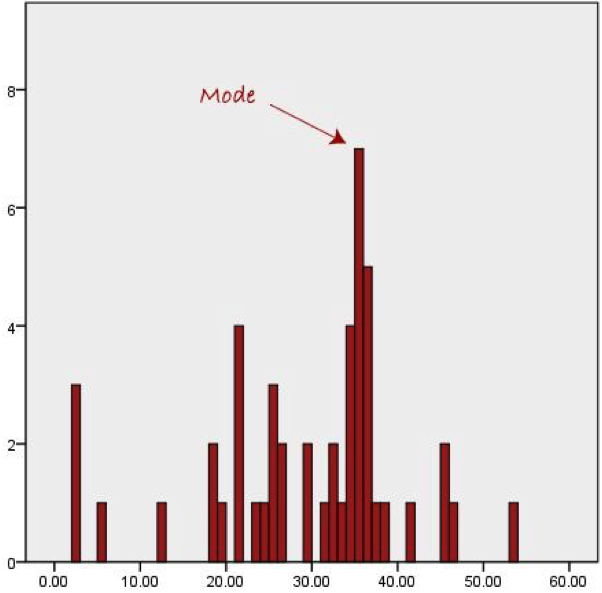
上面就是文档的大体翻译了,估计有些地方应该还是有些不太清楚。
阅读文档时,我发现平均数的表述用了mean,也用了average,于是网上搜罗了一番终于搞清楚。
统计学的范畴内,average有三种方式来表示:mean、mode、median。
mean是arithmetical mean,准确指一组数的“算术平均值”或“算术平均数”,也就是日常生活中理解的平均数;
mode指一组数据的众数,是一组数据中出现次数最多的那个数;
median指一组数据的中位数或中值,是把一组数据按照大小顺序排列好后,处在中间位置的那个数。
统计学在分析数据时,需要对数据进行最基础的描述性分析。在众多描述分析的指标中,平均数指标能够反映分布数列集中趋势.
平均数指标有两类:数值平均数,位置平均数。
数值平均数用mean表示;位置平均数用mode和median表示,因为它们能大概指出数据的平均数。
所以,当average表示数值平均数时,意思和mean是一样的;但是当表示位置平均数时,就是mode和median了。

